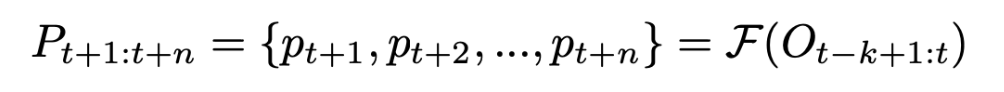
- 这边的pt = [Lont, Latt, Altt, V xt, V yt, V zt] 包含了经纬度海拔,及其对应向量
- 由于这边是飞行任务,需要海拔,对于路面数据,只需经纬度
- 文章的问题是给定n给$p_t$,输出未来n步
文章讲飞行轨迹预测任务转化为一个多元二分类任务,也就是讲经纬度变成二元序列,但是二元序列的高位会导致误差巨大,以及在推理过程中出现的误差叠加的情况。
MODEL
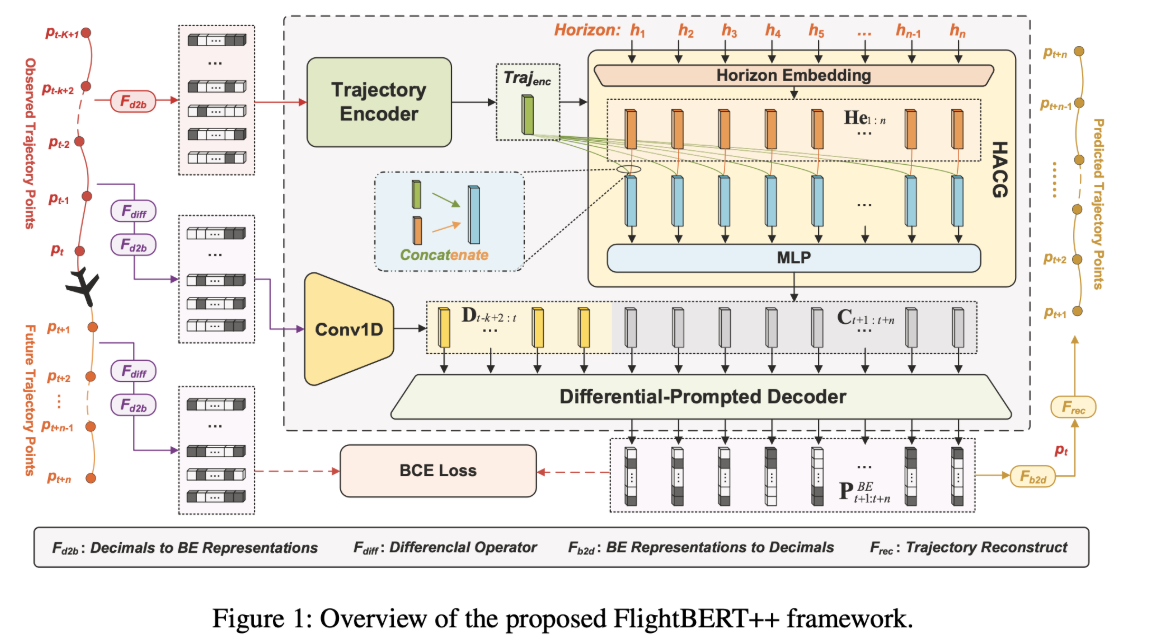
输入: - Observed Trajectory Points (Pt-k+1, …, Pt): 表示观测到的历史飞行轨迹点序列。下标 t-k+1 表示序列的起始时间点, t 表示当前时间点。 - Future Trajectory Points (Pt+1, …, Pt+n): 表示需要预测的未来飞行轨迹点序列。注意,在训练阶段会使用真实的未来轨迹点,用于计算损失并优化模型,而在预测阶段,这些点是未知的,需要模型来预测。 - Fd2b: Decimals to BE Representations: 表示十进制转换为二进制编码,将经纬度等信息转换为BE。
Trajectory Encoder
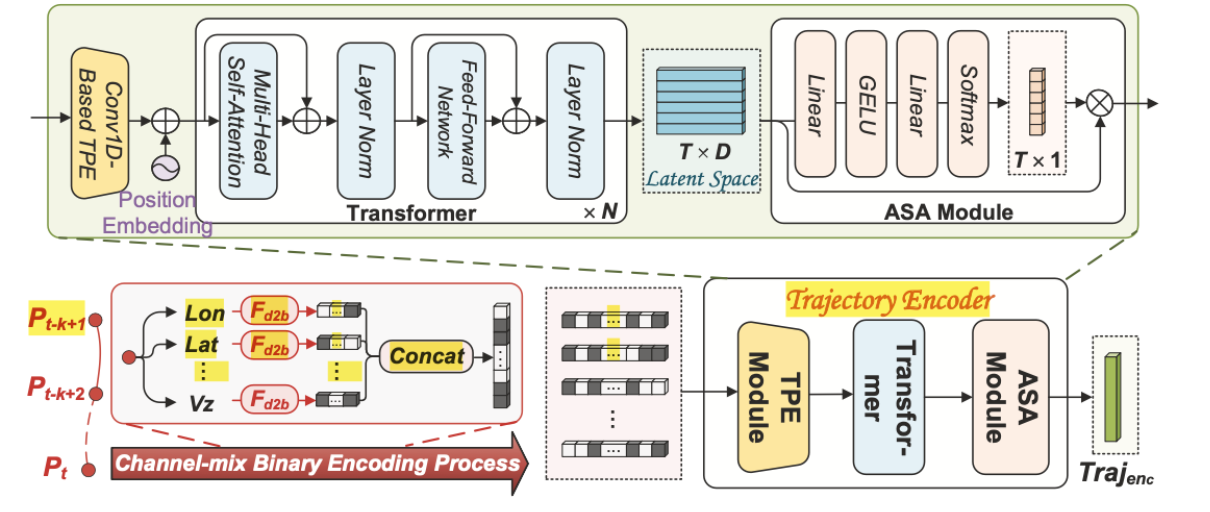
1. TPE 模块(Conv1D Embedding):
把每个 BE 表示的轨迹点用 1D 卷积映射到高维空间,得到:
\[E_t = \text{Conv1D}(BE(p_t))\]2. TTM 模块(Transformer):
对整个时间序列进行建模,学习轨迹之间的时序依赖关系:
\[Z = \text{Transformer}(E_{t-k+1}, …, E_t)\]将 Transformer 输出的所有时间步表示做加权求和,形成一个轨迹级别的表示:
\[\text{Traj}{enc} = \sum{i=1}^{k} \alpha_i Z_i \quad \text{(由注意力决定权重)}\]HACG(Horizon-Aware Context Generator)
编码预测时间步(Horizon):有点像位置编码
用 one-hot 编码预测的时间步(如 t+1, t+2, …, t+n),再嵌入成向量:
\[H = \text{HorizonEmbedding}([h_1, h_2, …, h_n])\]拼接轨迹信息与时间步信息,生成上下文:
\[c_{t+i} = \text{MLP}(\text{Concat}[\text{Traj}_{enc}, h_i])\]最终输出所有未来时间步的上下文:
\[C_{t+1:t+n} = \{c_{t+1}, …, c_{t+n}\}\]DPD(Differential-Prompted Decoder)
历史轨迹差分(即变化量)计算如下:
\[\Delta p_i = p_i - p_{i-1}\]然后用 BE 编码 → 输入到 Conv1D 网络,形成差分提示向量:
\[D_{t-k+2:t} = \text{Conv1D}(BE(\Delta p_{t-k+2}, …, \Delta p_t))\]拼接差分提示 + 上下文信息:
\[\text{Input}{decoder} = \text{Concat}[D_{t-k+2:t}, C_{t+1:t+n}]\]Masked Transformer 解码器处理: 建模预测差分值的时序依赖:
\[\hat{\Delta P}{BE} = \text{MaskedTransformer}(\text{Input}{decoder})\]输出差分(BE编码)→ 解码为数值 → 累加还原轨迹:
\[\hat{\Delta P}{t+1:t+n} = \text{DecodeFromBE}(\hat{\Delta P}{BE})\] \[\hat{P}_{t+1:t+n} = p_t + \sum \hat{\Delta P}\]- 输出差分,依次累加获得序列
为了减少BE representation的高比特预测误差,我们将差分预测范式(differential prediction paradigm)引入到FlightBERT++框架中,即解码器的目标是预测差分值(differential values)而不是原始绝对值(raw absolute values)。然而,从观测序列(observations sequence)中学习差分序列(differential sequence)的转移模式是具有挑战性的,因为差分运算(differential operation)可能会忽略轨迹属性(trajectory attributes)的一些地理和运动学特征
💥 为什么差分预测误差更小?
✅ 原因一:
变化量通常数值更小,便于建模
- 原始值可能范围大(如高度范围 0–13,000 米,经度从 70°–130°)
- 但两个相邻轨迹点之间的变化一般比较小(如经度只变化 0.001°,高度变动 30 米)
- 小数值 + 平稳变化 → 更容易学习和拟合!
🔍 类比:你很难学会“你一年赚多少钱”,但容易学会“你每个月多赚了多少钱”。
✅ 原因二:
BE 编码中的高位误差被削弱
举个例子:
-
绝对值用 BE 编码表示,比如 01100100 是 100。
- 如果预测错了第一个高位 → 值可能从 100 → 228(严重错误)
-
差分值范围小,只用更少的 bit 表示,比如 00000100 是 +4。
- 就算出错,也不太可能跳跃很远 → 预测更鲁棒。
📉 差分预测减少了高位的参与程度,大幅降低 BE高位错误带来的巨大数值跳跃风险。
✅ 原因三:
差分序列更“平稳”
在时间序列预测中,平稳性越强越容易预测。
差分操作通常会:
- 消除趋势项
- 消除绝对值的漂移
- 强化局部变化模式
🎯 平稳 → 模型容易学习出规律 → 误差更小
✅ 原因四:
误差不会像自回归那样叠加
FlightBERT++ 是非自回归的,同时使用差分预测:
- 每一步是独立预测,不依赖前一个预测
- 差分量小,误差积累更慢,整体误差分布更窄