轨迹分析的一项基本任务是轨迹表征学习(Trajectory Representation Learning, TRL),其目标是从高维原始轨迹数据中学习轨迹的低维且有意义的表征。
Motivation
- 目前的轨迹表示学习是基于这两个方法:基于网格的方法和基于道路的方法,这两个方法,两种模态在本质上是不同的,因此能够捕捉不同的轨迹特征并具有独特的优势。同时目前缺乏这两个模态的对比研究
- 此外,当前的路网表征学习(TRL)方法在很大程度上忽略了时空动态性。尽管最近的一些方法已经纳入了时间数据,但它们仍然将路网视为静态的这种局限性阻碍了关键时空模式的提取,例如高峰时段交通状况的剧烈变化。这些动态因素极大地影响了下游应用,如行程时间估计,这突显了在路网表征学习方法中融入时空动态性的必要性。
- 基于我们之前的观察,我们发现了两个主要挑战:(1) 网格(grid)与道路模态(road modality)之间的异构性。两种模态使用了完全不同的空间离散化方法,因此难以直接组合或融合这两种类型的信息。(2) 时空动态性(Spatio-temporal dynamics)。城市交通具有高度的动态性,并且随时间和空间的变化而显著不同。有效地建模这些动态变化极具挑战性。
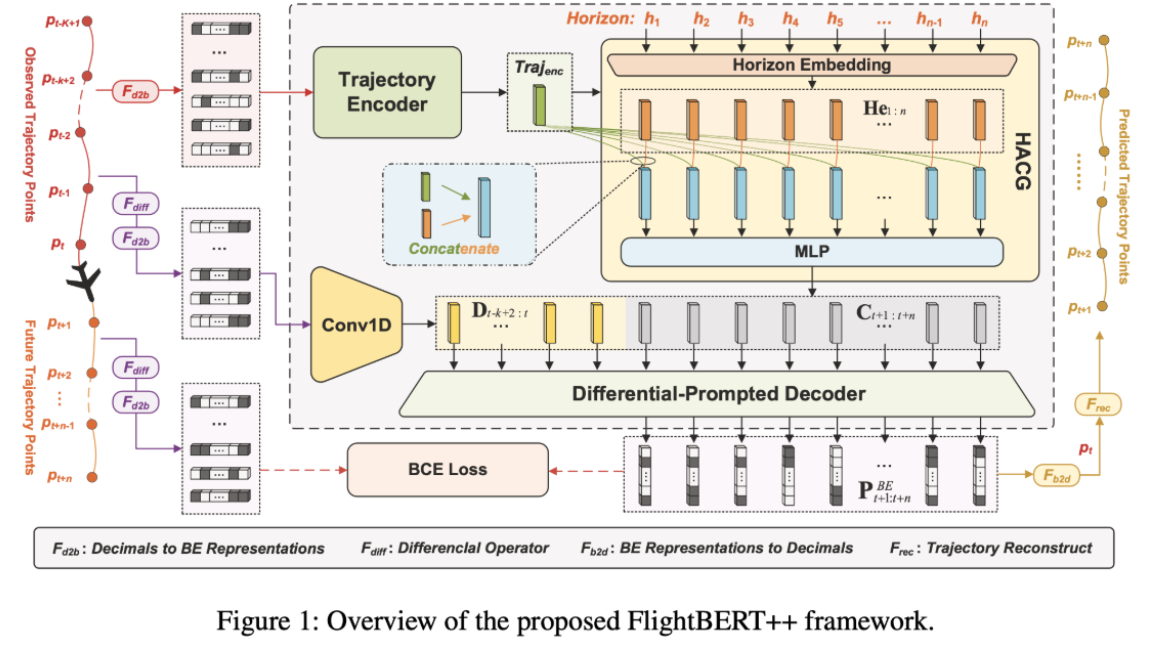
- 为了应对这些挑战,TIGR采用了一种三分支架构,并行处理网格数据、道路网络数据以及时空动态信息。其中,网格分支和道路分支代表了我们两个主要模态(modalities),而时空分支则提取源自道路模态的动态交通模式。我们将每个分支嵌入到潜在轨迹表征(latent trajectory representations)中,并在不同分支内(模态内,intra-modal)和分支间(模态间,inter-modal)对齐这些表征。通过结合这三个组成部分,TIGR能够更精细地提取多样的轨迹特征。这种集成方法使得我们的模型能够充分利用基于网格和基于道路的方法的优势,同时考虑到城市交通的动态特性。
Problem Definition
给定一个轨迹集合$\mathcal{D}={T_i}$,轨迹表征学习的任务是学习一个轨迹编码器 F : T → z,该编码器将轨迹 T 嵌入到一个通用的表征 z ∈$\mathbb{R}^d$ 中,其中 d 是表征的维度。该表征 z 应该准确地代表轨迹 T,并适用于各种下游应用,例如轨迹相似度计算、旅行时间估计和目的地预测。为此,轨迹编码器以无监督的方式进行训练。
方法
方法主要由三个核心部分组成:动态交通嵌入(dynamic traffic embedding)、时间嵌入(temporal embedding)以及通过局部多头注意力机制(local multi-head attention)进行的融合。
dynamic traffic embedding
对于两个相连的路段 vi 和 vj,其转移概率 (transition probability) 由 P[i,j] 给出,并通过历史轨迹计算得出。
\[P_{[i,j]}=\frac{\#transitions(v_i\to v_j)+1}{\#total\_visits(v_i)+|\mathcal{N}(v_i)|}\]其中$\mathcal{N}(v_i)$是vi的邻居个数,接下来对$P^{\prime}=D^{-1}(P+I)$规范化,D为度矩阵,I为单位矩阵
\[\mathbf{h}_i=P_{[i,i]}^{\prime}w_i\mathbf{x}_i^{(t_d,t_h)}+\sum_{v_j\in\mathcal{N}(v_i)}P_{[i,j]}^{\prime}w_j\mathbf{x}_j^{t_h},\]其中,N是邻域函数(neighbor function),返回一条道路的所有相邻道路;w是可学习的参数;$x^{t_h}$ ∈ X 表示第$t^h$小时的交通状态;hi是道路路段vi的动态交通嵌入(dynamic traffic embedding)。给定Tr中的道路序列,我们获得动态交通嵌入的序列$T^s = (h_1, h_2, h_3, . . . , h_{T^r})$。
Temporal Embedding
\[\mathbf{t}_i[k]=\begin{cases}w_kt_i+\phi_k&\mathrm{if~}k=0,\\\cos(w_kt_i+\phi_k)&\mathrm{else,}&\end{cases}\]其中,ti[k] 是维度为 q 的嵌入向量 ti ∈ Rq 的第 k 个元素,wk 和 ωk 是可学习的参数。捕捉周期模式。然后,我们将轨迹 Tr 的时间嵌入序列定义为 Tt = (t1, t2, t3, . . . , t_|Tr|)。
Fusion via Local Multi-Head Attention
为了融合动态交通嵌入 Ts 和时间嵌入 Tt,我们利用多头注意力机制(multi-head attention),并进行了一项特定的调整。该调整基于这样的直觉:在较小的时空窗口内的交通往往非常相似,而不同道路或不同时间的交通可能差异显著。因此,我们不希望注意力机制关注整个序列。相反,我们利用多头注意力机制中的每个独立“头”(head)对特定的子序列执行局部注意力(local attention),并提出了局部多头注意力机制(local multi-head attention)LMA。
\[LMA(Q,K,V)=[Att_1||Att_2||\ldots||Att_{|H|}]W^O\] \[\mathbf{T}^{st}=LMA(\mathbf{T}^s,\mathbf{T}^t,\mathbf{T}^t)\|LMA(\mathbf{T}^t,\mathbf{T}^s,\mathbf{T}^s).\]- 交叉注意力融合前面两个embedding
MASK
在嵌入每个分支后,我们为每个分支 b ∈ {g, r, st} 获得一个token embeddings序列 Tb。接下来,我们通过随机丢弃一些令牌来应用掩码(masking),并为每个分支获得两个不同的视图:Tb(视图 1)和 Tb(视图 2)。掩码的作用是双重的。首先,我们获得同一数据实例的两个不同视图,以指导每个分支内的对比学习(contrastive learning)。类似于掩码自编码器(masked autoencoders,MAE学习表征的方式,编码器必须理解空间关系并学习轨迹的内在信息,即潜在的路线。我们研究了三种掩码策略:
- Random masking (RM) 随机选一个字集然后以一定比例mask
- Consecutive masking (CM):选择连续点进行mask ,我们在轨迹中选择连续数量的点,其中点的数量由轨迹长度 |Tm| 的比例 pCM决定。
- 截断(Truncation, TC):类似地,我们可以对轨迹 Tm 的起点或终点处的连续点进行掩码处理,从而导致轨迹的截断。参数 pTC 定义了被掩盖点的比例。
Encoder
方法采用了两种类型的编码器:一个目标编码器(target encoder)以及一个锚点编码器(anchor encoder),这两个编码器具有不同的参数,其中目标编码器的参数$\tilde{\theta}$使用锚点编码器的参数$\theta$的指数移动平均(EMA)进行更新:$\tilde{\theta}\leftarrow\mu\tilde{\theta}+(1-\mu)\theta$,其中µ是一个目标衰减率(target decay rate)。这种EMA更新确保了更稳定的学习目标,并防止表征坍塌(representation collapse)。
在编码器架构方面,我们的设计基于Transformer,并进行了一些特定的增强。 我们采用了旋转位置嵌入(Rotary Positional Embeddings, RoPE) 在注意力机制中捕捉相对位置信息,从而改进了仅表示绝对位置的标准位置嵌入。此外,我们采用均方根层归一化(Root Mean Square Layer Normalization, RMSNorm),并将其应用于多头注意力机制和前馈层之前,而非之后。这一修改进一步稳定了训练过程。为了从每个分支获得最终的轨迹表示,我们对Transformer最后一层的输出序列进行均值池化(mean pooling)。这些架构上的选择使得我们的编码器能够有效地捕捉轨迹数据中复杂的空间和时间关系。
Inter- and Intra-Modal Losses
接下来,我们将每个表征通过一个投影头(projection head)进行投影,该投影头被建模为一个多层感知机(MLP)。使用投影头可以提高对比学习的性能, [28]。在$\tilde{z}^b$ 和 ˆzb 投影之后,我们得到 ˜pb 和 ˆpb。我们在每个分支内(模态内,intra-modal)和跨分支(跨模态,inter-modal)采用对比目标(contrastive objective),以学习丰富的、多样的表征,这些表征能够捕捉来自两种模态以及时空成分的互补信息。对于对比目标,我们利用 InfoNCE 损失
\[\mathcal{L}(x,y)=-\log\frac{\exp(x\cdot y/\tau)}{\sum_{j=0}^{|\mathcal{Q}_{neg}|}\exp(x\cdot y_j/\tau)+\exp(x\cdot y/\tau)},\]$\tau$是温度系数,$\mathcal{Q_{neg}}$是负样本,它在每次迭代中都会更新,以维持一个大型的负样本集合。在每次迭代时,我们将当前批次的样本入队(enqueue),并将队列中最老批次的样本出队(dequeue)。然后,我们在每个分支内(模态内,intra-modal)和不同分支之间(模态间,inter-modal)对齐视图:
Intra-modal contrastive learning实现了各分支内部的对齐。
\[\mathcal{L}^{intra}={}^1/3\sum_{\begin{array}{c}m\in\\\{g,r,st\}\end{array}}\mathcal{L}(\mathbf{\tilde{p}}^b,\mathbf{\hat{p}}^b).\]Inter-modal contrastive learning 有助于对齐各个分支。我们对比两种结构分支的投影,即˜pg和ˆpr,以及两种基于道路网络模态的分支,即˜pr和ˆpst。我们将跨模态损失定义为:
\[\mathcal{L}^{inter}={}^1/2[\mathcal{L}(\mathbf{\tilde{p}}^g,\mathbf{\hat{p}}^r)+\mathcal{L}(\mathbf{\tilde{p}}^r,\mathbf{\hat{p}}^{st})].\]最后的损失函数
\[\mathcal{L}_{TIGR}=\lambda\mathcal{L}^{intra}+(1-\lambda)\mathcal{L}^{inter}.\]- 时空分支(spatio-temporal branch,st)基于道路网络交通信息,因此与网格模态(grid modality,g)截然不同。 经验性地对齐这两个分支会降低所学习的轨迹表征的质量。
downstream application
训练完成后,为了获得轨迹的最终表示 z,我们使用训练好的轨迹编码器对每个分支的嵌入序列进行编码,并舍弃掩码和投影头。
\[\mathbf{z}^g=\mathrm{F}_\theta^\mathrm{g}(\mathbf{T}^g),\mathbf{z}^r=\mathrm{F}_\theta^\mathrm{r}(\mathbf{T}^r),\mathbf{z}^{st}=\mathrm{F}_\theta^\mathrm{st}(\mathbf{T}^{st}).\]最终表示:
\[\mathbf{z}=\mathbf{z}^{g}||\mathbf{z}^{r}||\mathbf{z}^{st}.\]实验
-
数据集 (Datasets):
-
使用了两个真实的、公开的出租车轨迹数据集:
-
波尔图 (Porto): 约 160 万条轨迹 (2013.7 - 2014.6)。
-
旧金山 (San Francisco): 约 60 万条轨迹 (2008.5 - 2008.6)。
-
-
相应的路网从 OpenStreetMap (开放街道地图) 提取。
-
数据预处理: 移除了城市边界外的轨迹,丢弃了过短 (<20点) 或过长 (>200点) 的轨迹,并使用 Fast Map Matching (FMM) 算法将轨迹点匹配到路网的道路段上。
-
-
对比方法 (Baselines):
-
选择了一些当前先进的轨迹表示学习 (TRL) 方法进行比较,分为两类:
-
基于网格 (Grid-based): t2vec, CLT-Sim, TrajCL, CSTTE。这些方法将轨迹表示为网格单元的序列。
-
基于路网 (Road Network-based): Trembr, Toast, JCLRNT, LightPath, START。这些方法将轨迹表示为道路段的序列。
-
-
简单的 Transformer 基线 (TF^g, TF^r): 作者还加入了在网格序列 (TF^g) 或路网序列 (TF^r) 上使用对比学习训练的基础 Transformer 模型,以便在相似的基础架构上直接比较两种模态。
-
选择标准: 选择的基线都是自监督训练的,能学习用于多种下游任务的通用表示(与 TIGR 类似)。
-
-
下游任务 (Downstream Tasks):
-
使用三个常见的任务来评估学习到的轨迹表示的质量:
-
轨迹相似度 (TS - Trajectory Similarity): 给定一个查询轨迹,在数据库中找到最相似的轨迹。设置:将轨迹拆分为奇数点(查询)和偶数点(数据库项),并加入大量负样本 (k_neg) 增加难度。指标:平均排名 (MR↓),命中率@1/5 (HR@1/5↑)。
-
行驶时间估计 (TTE - Travel Time Estimation): 预测轨迹的总行驶时间。在学习到的表示上训练一个 MLP 预测器(只使用开始时间以避免信息泄露)。指标:平均绝对误差 (MAE↓),平均绝对百分比误差 (MAPE↓),均方根误差 (RMSE↓)。
-
目的地预测 (DP - Destination Prediction): 给定轨迹的前 90%,预测其最终的道路段。在部分轨迹的表示上训练一个 MLP 预测器。指标:F1 分数 (F1↑),准确率@1/5 (Acc@1/5↑)。
-
-
评估协议: 对于所有下游任务,TRL 模型(TIGR 和基线)在预训练后参数被冻结,只在其输出的表示(embeddings)之上训练一个简单的 MLP 预测器。这能更好地衡量表示本身的质量。
-
-
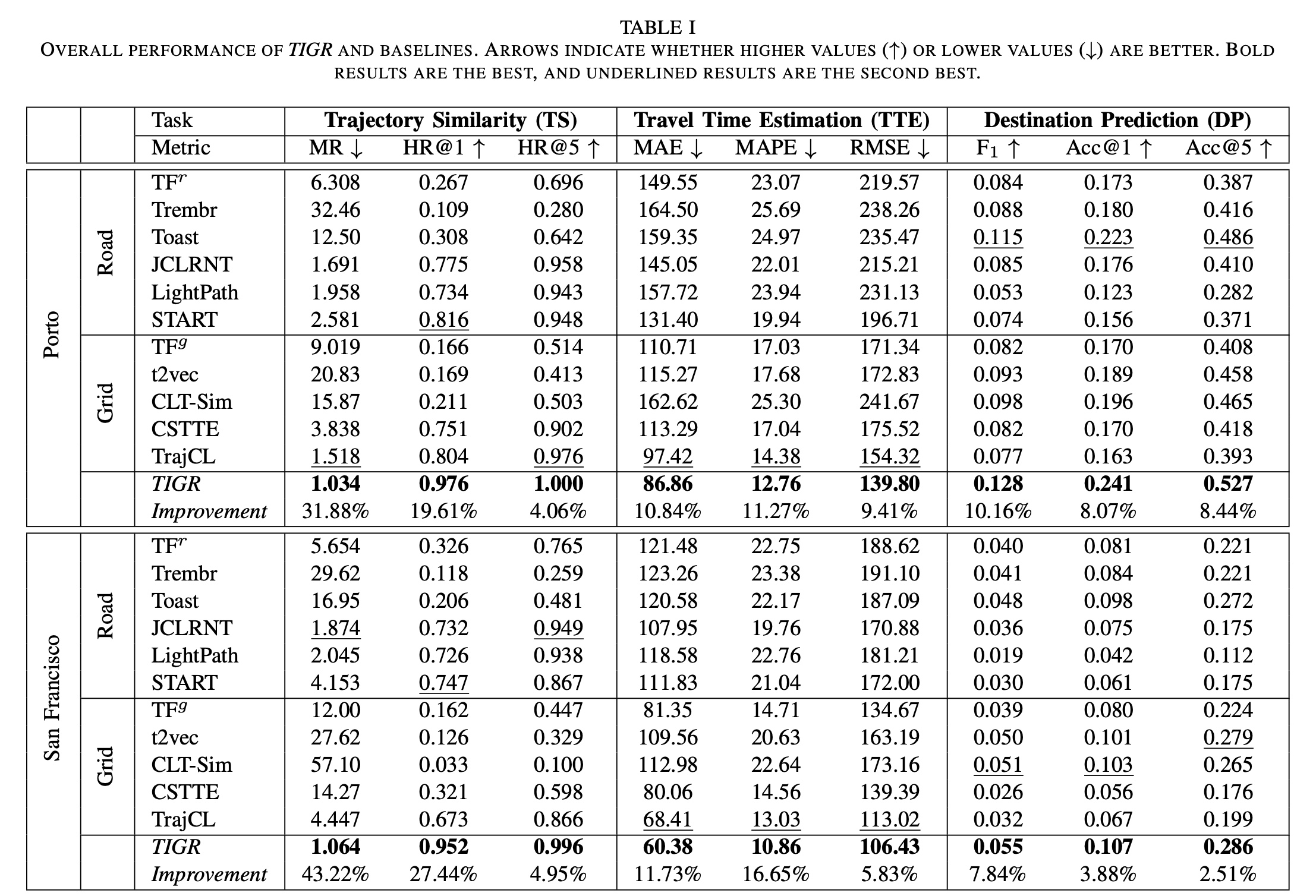
整体性能 (Overall Performance - 表 I):
-
TIGR 在几乎所有指标上,均显著优于所有对比方法,覆盖了全部三个任务和两个数据集。
-
性能提升非常显著,尤其是在 TS 任务上 (最高提升 43.22%),在 TTE (最高 16.65%) 和 DP (最高 10.16%) 上也很明显。
-
结论: 整合网格、路网和时空动态信息能够学习到更优越、更通用的轨迹表示。
-
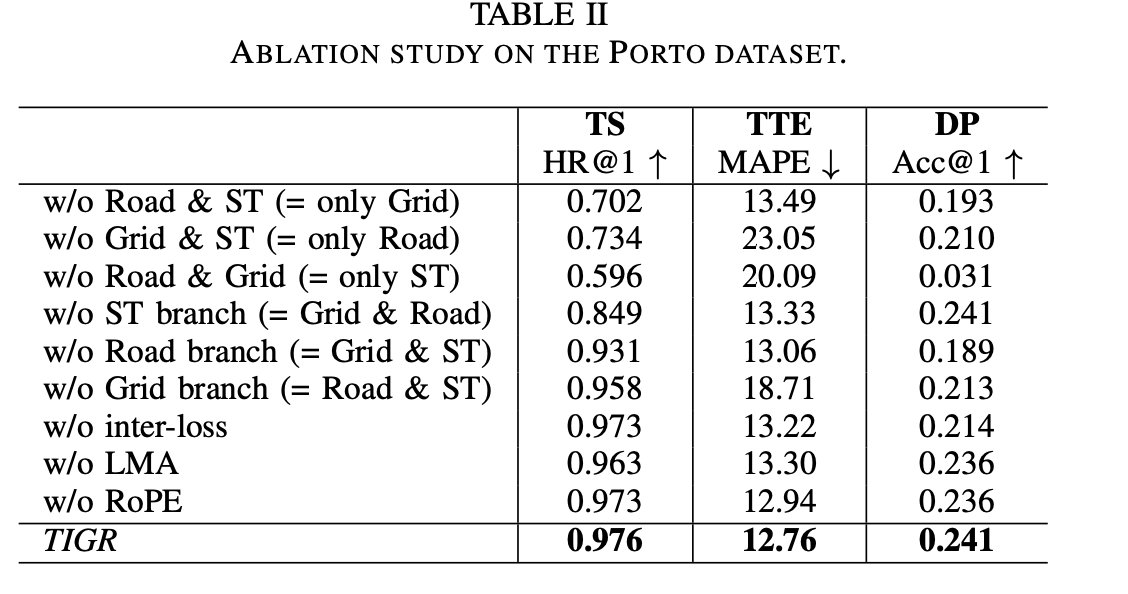
- 可以发现路网和网格影响巨大
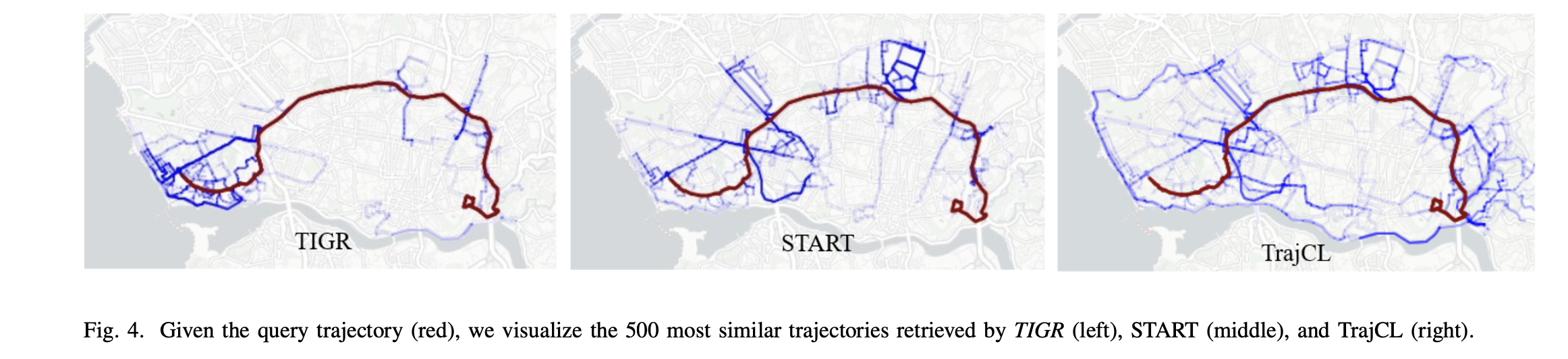
可视化